音高 (PITCH) と音律

【可聴周波数について】

人の耳に聞こえる可聴周波数は、低音域で20Hz、高音域で20kHzと言われていますが、その聞こえる音域内において、古代ギリシャの数学者ピタゴラスによって「音律」というものが作られました。

以下PITCHとは周波数（１秒間の振動数）のことを指し、Hz（ヘルツ）という単位で記されます。

【音律について】

ここでは現代の西洋音楽で使用される、いわゆる「ドレミ」の音階がどのようにして作られたのかを見ていきましょう。

まず１つの基準となるPITCH（ピッチ）（下図０１の x ）を設定します。そこから見て最も調和の取れたPITCHはユニゾン（基準となるPITCHそのまま）です。

そしてその次に調和度の高いPITCHが発見されました。それは現代でオクターブ上と呼ばれる位置にあり、基準音程から見て２倍の振動数を持つPITCHです。下（図０１）ではそれを x1 と記します。

また x1 は x から見て２倍の振動数を持っていますので、１：２（ x1は x の２倍）ということになり、同じく x1 に対して１：２の位置に x2 があり、その後 x3、x4 と更にオクターブ毎にPITCHの上昇が確認されました。

（図０１）

図01の x に対して x はUnison（ユニゾン＝同じ音程）は１：１の比率、

x に対して x1 は１：２の比率（２倍の周波数）、x1 に対して x2 もまた１：２の比率です。

ここで図０１及で使用した x に周波数（ここでは仮にC音を264Hzに設定することにします。）を当てはめた場合、

x = 264Hz、 x1= 528Hz (264×2÷1) 、 x2 = 1056Hz (528×2÷1)、 

x3 = 2112Hz (1056×2÷1)、 x4 = 4224Hz (2112×2÷1)、x5 = 8448Hz (4224×2÷1)

ここでわかることは、PITCHがオクターブ上がるにつれて隣り合うPITCH同士の周波数の差が大きくなります。

その次に調和度の高い音程としてxに対して３倍の位置に存在するPITCHが発見されました。

つまり基準となるPITCHの３倍の場所に位置するPITCHで792Hz (264×3)になります。

🔳ここからxとx１の間に入るPITCHを見ていきます。🔳

先ほどのは792Hzは、図０１において x1 と x2 の中間に位置する音程（x1以上の周波数）であるため、それを半分に割ります。その結果396Hzという数値が導き出されました。これは 

x (264Hz)に対して２：３の比率になります。(264×3÷2=396)

図０２に示すように、これも x から見て２：３、x1 から見て２：３、また y 同士は１：２の比率で延々と続いていきます。

また図０２ではその音程を y と記します。そして　x ( ) と x ( )の中間に位置するという特徴から、 x と x1 の間に y を配置します。

（図０２）

ここまでで導出された周波数は

x = 264Hz、 y = 396Hz、 x1 = 528Hz

加えて y の値は、

y = 396Hz、 y2 = 792Hz、 y3 = 1584Hz、 y4 = 3168Hz、 y5 = 6336Hz

次にこれら以外のPITCHを探していきます。（周波数の小さな数値順で記載）　

1. y1 に対してその半分の周波数（２：１の割合）の数値は、594÷２×1=297Hz

(b) y3 に対して（２オクターブ下なので）半分の更に半分の数値、　　　　　　(1336.5÷2×1)÷2×1=334.125 ≒ 334.13Hz

(c) y5 に対して（４オクターブ下なので）８で割ると、3007.125÷8=375.89062 ≒ 375.89Hz

(d) y2 に対してその半分の周波数（２：１の割合）の数値、 891÷2×1=445.5Hz

(e) y4 に対して（３オクターブ下なので）４で割ると、2004.75÷4=501.1875 ≒ 501.19Hz

ここまでで導出された数値を昇順に整列するとこうなります。（仮に音名も書きます。）

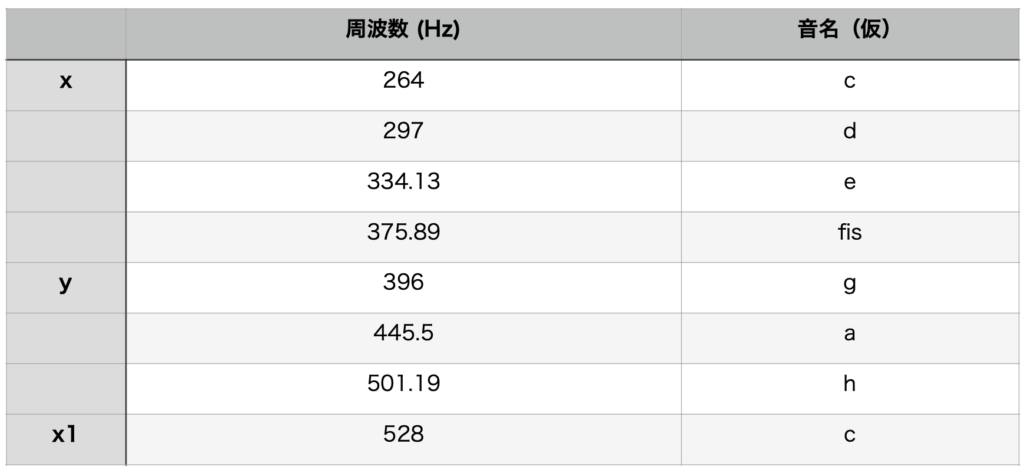
なぜここで４つ目の音名がF#になるのか、それは334.13Hzと396Hzのちょうど中間の数値は約365.06になり、375.89Hzはそれよりも高いためです。

これはリディアン・スケールに相当します。

つまり、リディアン・スケールは最も調和度の高い音程で構成された音階です。

またいわゆるメイジャー・スケールと呼ばれるアイオニアン・スケールに含まれるF音を数値で算出した場合、

264÷3×2=176 これに更に２をかけて、176×2=352Hz

となります。

次に　倍音列　について

倍音列 （OVERTONE SERIES）

例えば机をタップするなど、１つの「振動」が発音されると同時に倍音も鳴ります。

つまり１つのPITCHだけではなく、OCTAVE上のPITCHをはじめ、その他のPITCHも同時発音されています。

（図０３）

（これらのPITCHが同時発音されています。） 

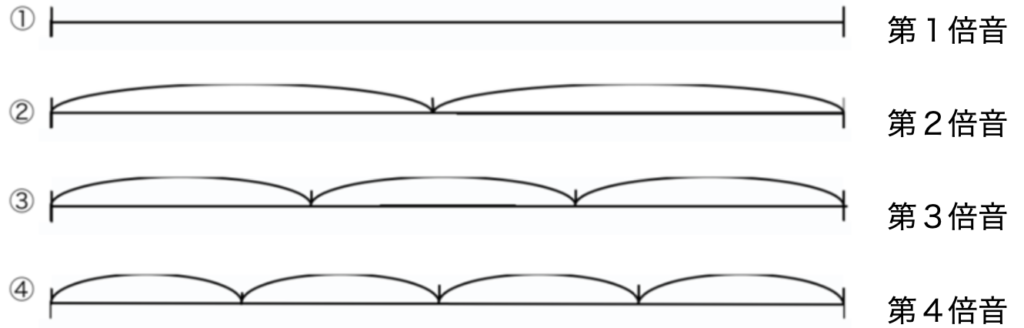
（図０４） 

• ※ここに f が発音されていないことに注目してください。

  また、第７倍音 (b) と 第11倍音 (fis) は少し低いです。

次に先ほど導出した各PITCH（一部近似値になりますが）を（図０５）にて各PITCH間の間隔の比率を数値化しました。

（図０５）

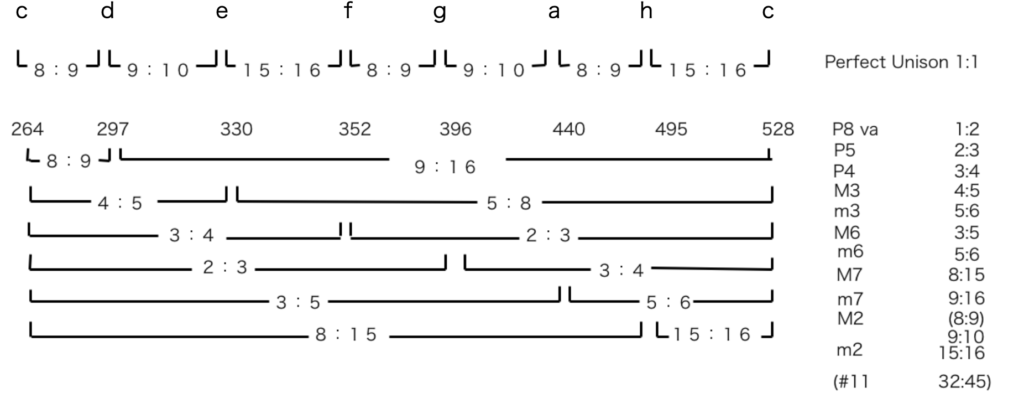
ここで初めて慣れ親しんだPITCH (A = 440Hz) が出てきましたね。

ここで注目していただきたいのが、

c d 間、d e 間は本来同じ比率になるべきなのにそうなっていないこと。

つまり各PITCHの周波数の間隔は均等にならないということです。言い換えれば、いわゆるドレミのHz（周波数）は整数にはなりません。つまり割り切れない数値ということです。

ここでは説明を割愛しますが、その後純正律、平均律などが作られました。私たちの身近にある楽器で言えばピアノは平均律で各音高が割り当てられています。また、ギターやエレキベース、マンドリン、バンジョーなどフレットのある弦楽器も多くの場合は平均律でチューニングされていますが、PITCHが完全に調整できない理由は、各弦によって異なる倍音列を持っているからです。クラシック音楽など、交響楽などは純正律が使われることが一般的です。それは各調において各PITCHを最も聴覚上快適なHz（周波数）にすることを目的とされ、平均律に生じる違和感を回避するためでもあると言われています。

またここで紹介させていただく音率は西洋音楽式のものですが、世界にはたくさんの音率が存在します。そしてここで語らせていただく音楽理論、コード理論の発端は、太古の昔、メロディーには伴奏もなく、ただ単音で演奏されるものでした。これをモノフォニーといいます。その後２つのPITCHを同時に存在させると、よりメロディーが豊かになるという方法が生まれました。これをポリフォニーといいます。そこから現代のように和声という概念が生まれ、多彩な和音に彩られたホモフォニーへと形を変えてきました。そのように世界中の地域には個々の歴史的背景を基にそれぞれの音楽が形作られています。